Lý thuyết và những dạng bài tập về Dấu hiệu nhận biết tiếp tuyến của đường tròn

Dấu hiệu nhận biết tiếp tuyến của đường tròn là kiến thức rất quan trọng trong chương trình Toán hình học lớp 9. Đặc biệt, đây còn là dạng bài hay xuất hiện trong các bài kiểm tra, ôn tập. Vậy nên, bài viết này sẽ giúp các em học sinh hiểu rõ hơn về khái niệm, các định lý, các dạng bài tập về tiếp tuyến.

Các bài viết tham khảo thêm:

• Sự xác định đường tròn. Tính chất đối xứng của đường tròn

• Đường kính và dây của đường tròn

• Liên hệ giữa dây và khoảng cách từ tâm đến dây

I. Kiến thức cần nhớ về dấu hiệu nhận biết tiếp tuyến của đường tròn

1. Nhận biết tiếp tuyến của đường tròn

Định lý: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

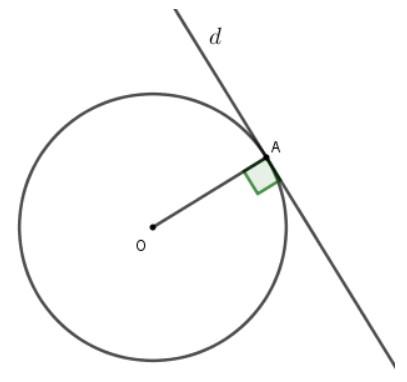
Ngoài ra, chúng ta cần nhắc lại một số dấu hiệu đã biết:

• Nếu một đường thẳng và một đường tròn chỉ sở hữu một điểm chung thì đường thẳng đó chính là tiếp tuyến của đường tròn.
• Nếu khoảng cách từ tâm một đường tròn đến một đường thẳng bằng bán kính của đường tròn đó thì đường thẳng ấy là tiếp tuyến của đường tròn.

2. Tính chất của tiếp tuyến

• Nếu một đường thẳng chính là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm ấy.
• Nếu một đường thẳng đi qua một điểm trên đường tròn và vuông góc với bán kính đi qua điểm đó thì nó là một tiếp tuyến của đường tròn.

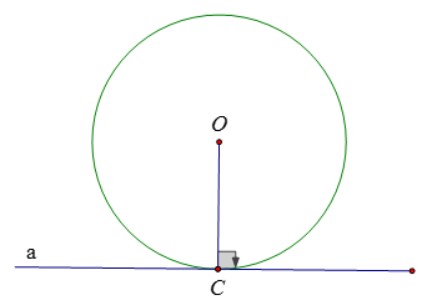
Trong hình trên a là tiếp tuyến của đường tròn (O ; C) => a vuông góc với OC tại C.

II. Những dạng bài tập về Dấu hiệu nhận biết tiếp tuyến của đường tròn

Dạng 1. Chứng minh một đường thẳng chính là tiếp tuyến của một đường tròn

Phương pháp giải: Để chứng minh được đường thẳng a chính là tiếp tuyến của đường tròn (O; R) tại tiếp điểm C, ta có thể áp dụng một trong các cách sau:

• Cách 1: Chứng minh điểm C nằm trên (O) và OC vuông góc với đường thẳng a tại điểm C.
• Cách 2: Kẻ OH vuông góc với đường thẳng a tại H và chứng minh rằng: OH = OC = R.
• Cách 3: Vẽ tiếp tuyến a’ của (O) và chứng minh đường thẳng a trùng với a’ (a a’).

Bài 1: Cho đường thẳng d và điểm A nằm trên d; B là điểm nằm ngoài d. Hãy dựng đường tròn tâm O đi qua điểm B và tiếp xúc với đường thẳng d tại điểm A.

Lời giải:

Trung trực AB cắt đường thẳng vuông góc với đường thẳng d ở điểm A tại (O) => Đường tròn (O;OA) là đường tròn cần dựng.

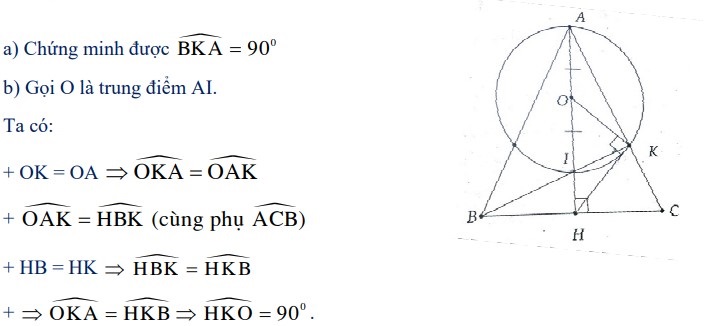
Bài 2: Cho ΔABC cân tại A, các đường cao AH và BK cắt nhau tại điểm I. Chứng minh:

a) Đường tròn có đường kính AI đi qua điểm K;

b) HK là tiếp tuyến của đường tròn có đường kính AI.

Lời giải:

Dạng 2. Tính độ dài

Phương pháp giải dạng bài toán tính độ dài: Nối tâm đường tròn với tiếp điểm để áp dụng định lý về tính chất của tiếp tuyến và vận dụng các công thức về hệ thức lượng trong tam giác vuông để tìm độ dài các đoạn thẳng.

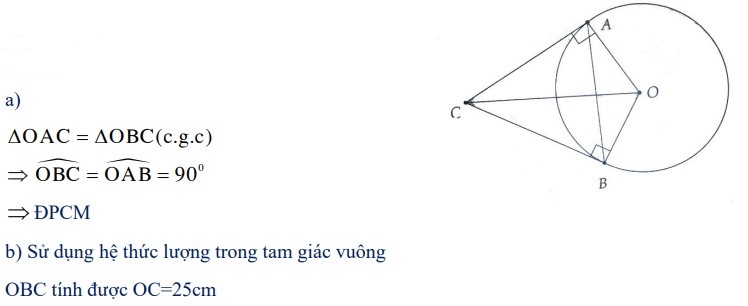
Bài 1: Cho đường tròn (O) có dây AB khác đường kính. Qua điểm O kẻ một đường vuông góc với đoạn thẳng AB, cắt tiếp tuyến tại A của đường tròn (O) ở điểm C.

a) Chứng minh đoạn thẳng CB là tiếp tuyến của đường tròn.

b) Cho bán kính của đường tròn tâm O bằng 15 cm và dây AB = 24 cm. Tính độ dài đoạn thẳng OC.

Lời giải:

Bài 2: Cho đường tròn tâm O, bán kính R và đường kính AB. Vẽ thêm dây AC sao cho góc CAB bằng 30 độ. Trên tia đối của tia BA, chọn điểm M sao cho BM = R. Chứng minh:

1. a) MC là tiếp tuyến của (O);
2. b) MC = R√3 .

Lời giải:

a) Vì ΔOCB đều nên BC = BO = BM = R => Góc OCM là góc vuông => MC là tiếp tuyến của (O).

b) Ta có:

OM² = OC² + MC² => MC² = 3R² => MC = R√3.

Dạng 3: Tổng hợp hai dạng trên (Nâng cao)

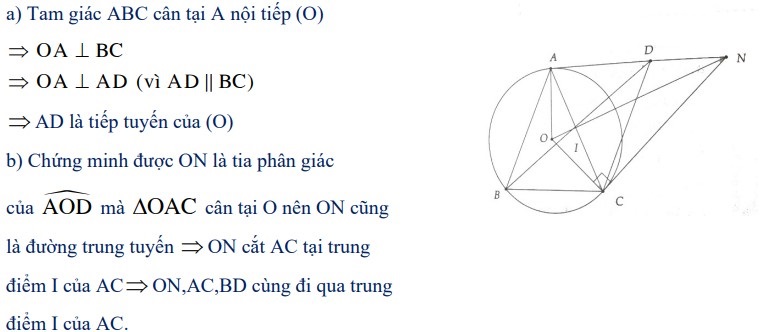
Bài 3: Cho Δ ABC cân tại A, nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại điểm C của đường tròn cắt đường thẳng AD tại điểm N. Chứng minh:

a) Đường thẳng AD là tiếp tuyến của đường tròn tâm O;

b) AC, BD, ON đồng quy với nhau.

Lời giải:

Bài 2: Cho nửa đường tròn tâm O đường kính AB và M là điểm nằm trên (O). Tiếp tuyến tại M cắt tiếp tuyến tại điểm A và điểm B của (O) lần lượt ở C và D. Đường thẳng AM cắt OC tại điểm E, đường thẳng BM cắt OD tại điểm.

a) Chứng minh góc COD là góc vuông.

b) Tứ giác MEOF là hình gì?

c) Chứng minh AB chính là tiếp tuyến của đường tròn đường kính CD.

Lời giải:

b) Do Δ AOM cân tại O nên OE là đường phân giác đồng thời là đường cao.

=> Góc OEM là góc vuông

Chứng minh tương tự, ta có góc OFM cũng là góc vuông => MEOF là hình chữ nhật.

C) Gọi I là trung điểm CD => I là tâm của đường tròn đường kính CD và IO = IC = ID. Có ABDC là hình thang vuông tại A và B nên IO // AC // BD và IO vuông góc với AB. Do đó AB chính là tiếp tuyến của đường tròn đường kính CD.

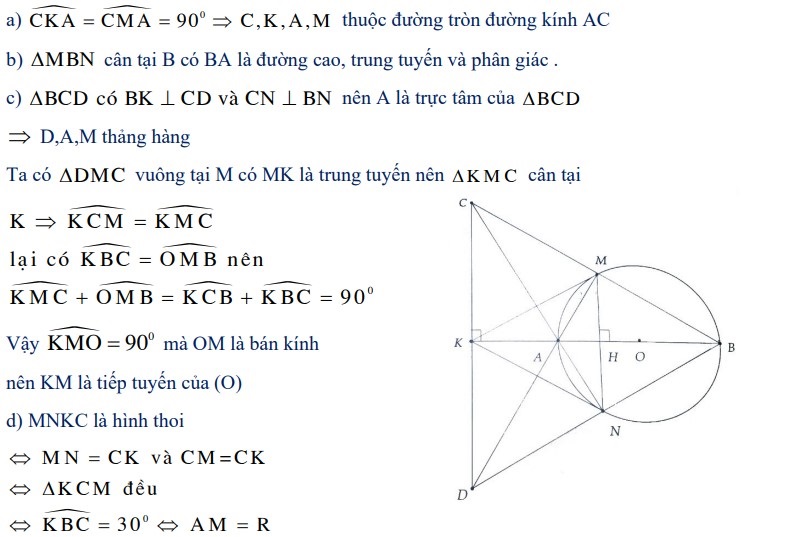
Bài 3: Cho đường tròn tâm O và đường kính AB. Lấy điểm M thuộc (O; AB) sao cho MA < MB. Vẽ dây MN vuông góc với AB tại điểm H. Đường thẳng AN cắt BM tại C. Đường thẳng qua điểm C vuông góc với AB tại điểm K và cắt BN tại D.

a) Chứng minh 4 điểm A, M, C và K cùng thuộc đường tròn.

b) Chứng minh tia BK là tia phân giác của góc MBN.

c) Chứng minh ΔKMC cân và KM là tiếp tuyến của (O).

d) Tìm vị trí của điểm M trên (O) để tứ giác MNKC trở thành hình thoi.

Lời giải:

Vậy là bài viết Dấu hiệu nhận biết tiếp tuyến của đường tròn kết thúc rồi đó. Hãy nhớ đọc kỹ những khái niệm, tính chất, cách ứng dụng để giải các bài toán lớp 9 về tiếp tuyến. Nhớ theo dõi và truy cập hoctot.hocmai.vn để cập nhật các bài học mới nhất. Chúc các em học tập tốt!