
Các cách tìm vecto pháp tuyến của một đường thẳng
Vecto pháp tuyến là một thuật ngữ thường được sử dụng rộng rãi trong lĩnh vực đại số tuyến tính và hình học. Tuy nhiên, không phải ai trong chúng ta cũng hiểu rõ về khái niệm này. Bài viết này sẽ cung cấp cho bạn đầy đủ các kiến thức cơ bản nhất về loại vecto này từ những khái niệm, tính chất, cho đến cách ứng dụng nó để “xử lý” một số bài toán. Hãy cùng tìm hiểu ngay!
Pháp tuyến là gì?
Trong hình học, pháp tuyến (hay trực giao) là một đối tượng như đường thẳng, tia hoặc vecto, vuông góc với một đối tượng nhất định. Ví dụ, trong hai chiều, đường pháp tuyến của một đường cong tại một điểm nhất định là đường thẳng vuông góc với đường tiếp tuyến với đường cong tại điểm đó.
Một vecto pháp tuyến có thể có chiều dài bằng một (một vecto pháp tuyến đơn vị) hoặc không. Dấu đại số của nó có thể biểu thị hai phía của bề mặt (bên trong hoặc bên ngoài).
Vecto pháp tuyến là gì?
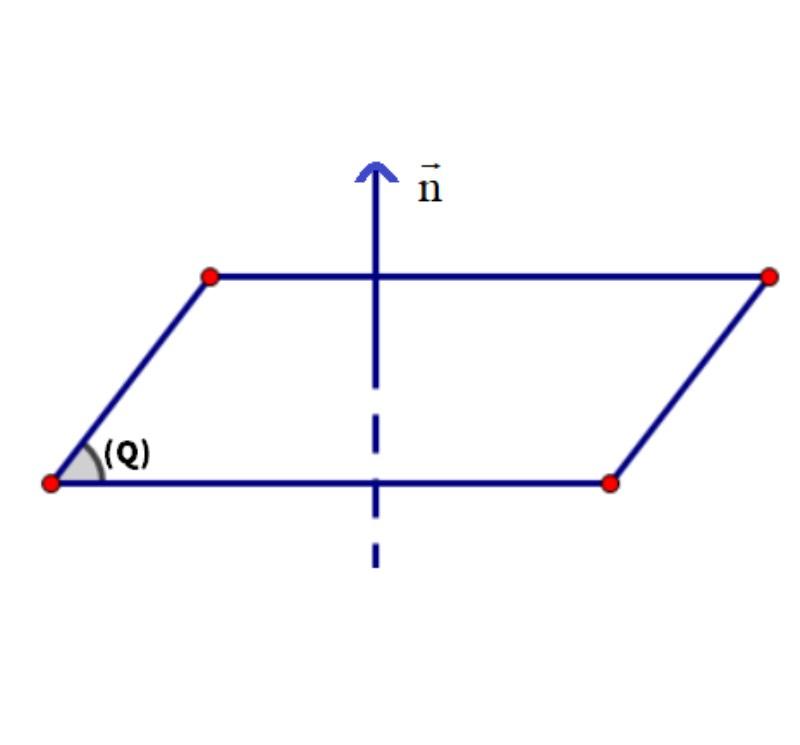
Theo định nghĩa, vecto pháp tuyến của một đường thẳng là một vecto vuông góc với đường thẳng đó và có độ dài khác 0. Ký hiệu: Vecto →n
Vecto →n được gọi là vecto pháp tuyến của đường thẳng ∆ nếu →n≠ →0 và →n vuông góc với vecto chỉ phương của ∆. Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vecto chỉ phương của đường thẳng đó.
Vecto →n là một khái niệm quan trọng trong đại số tuyến tính và hình học không gian. chúng được sử dụng để xác định hướng của mặt phẳng hoặc đường thẳng, tính toán phép chiếu và định hình không gian.
Tính chất của vecto pháp tuyến:
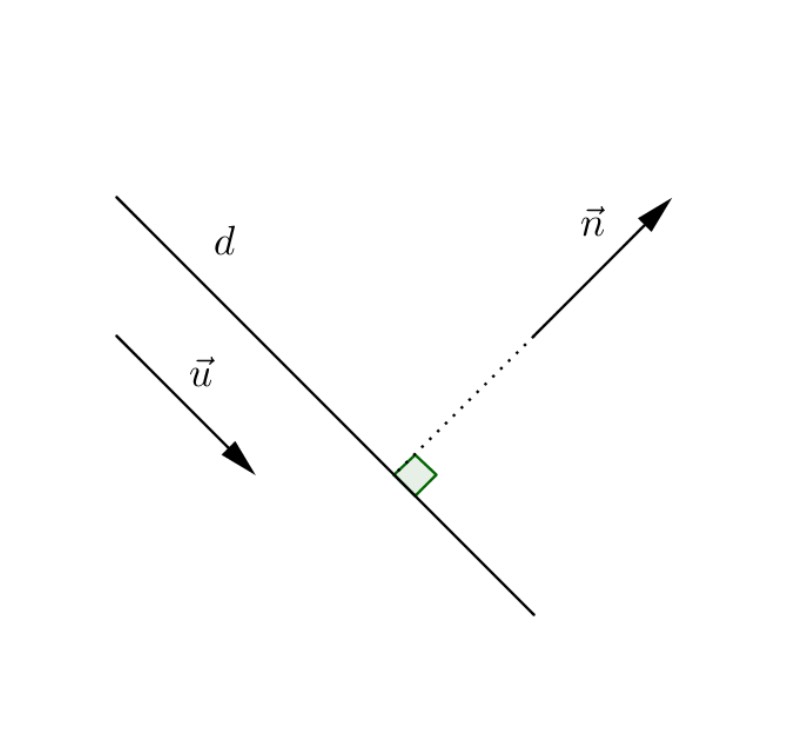
Tính chất của vecto →n đóng vai cực kỳ quan trọng trong lĩnh vực toán học bao gồm cả đại số và hình học. Bởi chỉ khi hiểu được đầy đủ tính chất của vecto, bạn mới có thể áp dụng nó một cách hiệu quả để giải quyết các bài toán.
Dưới đây là các tính chất cơ bản nhất của một vecto pháp tuyến mà bạn cần phải lưu ý:
- Mỗi đường thẳng trên mặt phẳng chỉ có duy nhất một vecto pháp tuyến (nếu không tính yếu tố hằng số dương).
- Nếu hai đường thẳng song song với nhau, thì vecto pháp tuyến của chúng cũng sẽ song song.
- Nếu hai đường thẳng vuông góc với nhau, thì vecto pháp tuyến của một đường thẳng sẽ song song với đường thẳng kia.
- Vecto pháp tuyến là vecto vuông góc với mặt phẳng hoặc đường cong tại điểm được xét.
- Độ dài của vecto pháp tuyến là độ dài ngắn nhất có thể của các vecto nằm trên mặt phẳng hoặc đường cong tại điểm được xét.
- Dấu của vecto pháp tuyến có thể biểu thị hai mặt của bề mặt (bên trong hoặc bên ngoài).
Cách tìm vecto pháp tuyến
Để hiểu rõ hơn về cách tìm vecto →n của một đường thẳng, bạn có thể tham khảo một trong các bài toán sau:
Từ phương trình tổng quát của đường thẳng
Khi một đường thẳng được biểu diễn dưới dạng ax + by + c = 0, vecto →n sẽ là n = (a;b).
Ví dụ minh hoạ:
Giả sử, có phương trình đường thẳng sau: 2x + 3y - 6 = 0. Để tìm vecto →n của đường thẳng này, ta chỉ cần lấy các hệ số của x và y trong phương trình. Trong trường hợp này, a = 2 và b = 3, vì vậy vecto →n sẽ là n = (2;3).
Từ vecto chỉ phương của đường thẳng
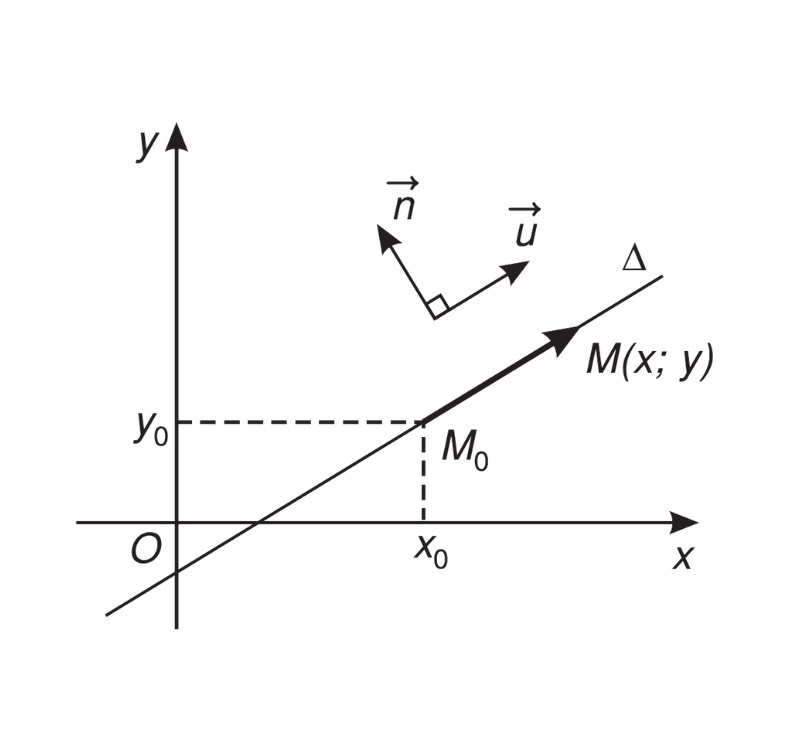
Đối với một đường thẳng có vecto chỉ phương là u = (a;b), vecto →n sẽ là n= (-b;a) hoặc n= (b;-a).
Ví dụ minh hoạ:
Nếu bạn có một đường thẳng với vecto chỉ phương là u = (2;-4), thì vecto →n là n = (-(-4);2) = (4;2) hoặc n = (2; -(-4)) = (2;4).
Từ tính chất vuông góc của hai đường thẳng
Nếu có một đường thẳng d vuông góc với một đường thẳng d’ có phương trình: ax + by + c = 0, vecto →n của d sẽ là n = (a;b).
Ví dụ minh hoạ:
Giả sử, có hai đường thẳng:
- Đường thẳng d có phương trình: 2x + 3y - 6 = 0.
- Đường thẳng d’ có phương trình: 3x - 2y + 4 = 0.
- Đường thẳng d’ có vecto chỉ phương là (u) = (3;-2).
Suy ra, vecto →n của đường thẳng d(n) sẽ vuông góc với vecto →u của đường thẳng d'(u), n = (-2;3).
Từ tính chất song song của hai đường thẳng
Nếu có một đường thẳng d song song với một đường thẳng d’ có vecto chỉ phương là u= (a;b), vecto →n của d sẽ là n = (-b;a), hoặc n = (b;-a).
Ví dụ minh hoạ:
Đường thẳng d’ có phương trình 2x - y + 4 = 0, vậy vecto chỉ phương của d’ là u = (2;-1). Suy ra, vecto →n của đường thẳng d (n) là:
n = (-(-1);2) = (1;2) hoặc n = (2;-(-1)) = (2;1).
Từ tích vô hướng
Đối với mặt phẳng, để tìm vecto →n, ta cần xác định hai vecto AB và AC của mặt phẳng đó, với A, B, C là ba điểm không thẳng hàng trên mặt phẳng. Sau đó, ta tìm tích vô hướng của hai vecto đó: AB x AC.
Ví dụ minh hoạ:
Giả sử chúng ta có một mặt phẳng được định bởi ba điểm A(1,2,3), B(2,3,4) và C(3,4,5) không thẳng hàng.
Để tìm vecto →n của mặt phẳng này, chúng ta sẽ thực hiện các bước sau:
- Xác định hai vecto AB và AC bằng cách trừ tọa độ của điểm cuối cho điểm đầu:
Vecto AB = B - A = (2 - 1, 3 - 2, 4 - 3) = (1,1,1).
Vecto AC = C - A = (3 - 1,4 - 2, 5 - 3) = (2, 2, 2).
- Tính tích vô hướng của hai vecto này (AB x AC):
AB x AC = (1,1,1) x (2,2,2) = ((1 * 2) - (1 * 2), (1 * 2) - (1 * 2), (1 * 2) - (1 * 2)) = (0,0,0).
Vậy vecto →n là vecto n = (0,0,0)
Kết luận
Vecto pháp tuyến là một khái niệm quan trọng và hữu ích trong nhiều lĩnh vực khoa học và kỹ thuật. Nó giúp chúng ta hiểu rõ hơn về sự biến thiên của đại lượng tại các điểm cụ thể và có ứng dụng đa dạng từ địa hình đến vật lý và toán học. Việc nắm vững khái niệm này có thể giúp chúng ta nắm bắt và giải quyết nhiều vấn đề phức tạp hơn trong các lĩnh vực hàng ngày.
Link nội dung: https://diendanxaydung.net.vn/vecto-phap-tuyen-a47902.html