
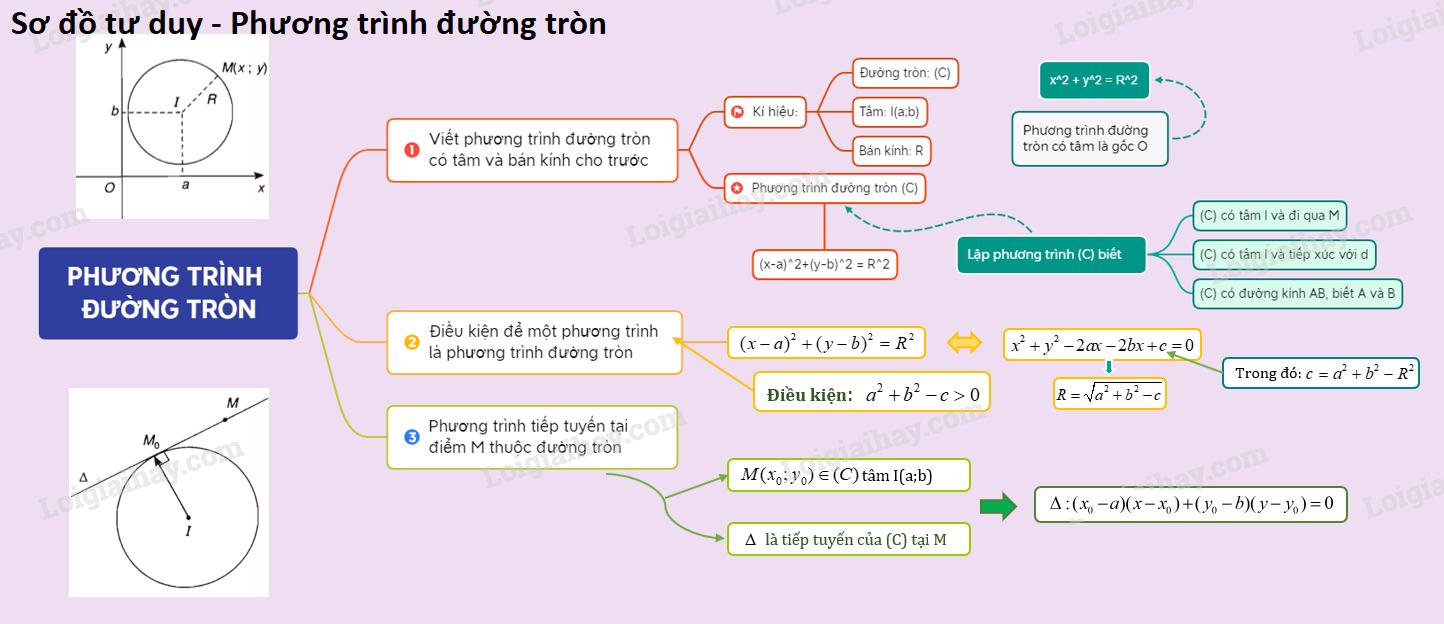
Lý thuyết phương trình đường tròn
1. Lập phương trình đường tròn có tâm và bán kính cho trước
Phương trình đường tròn có tâm (I(a; b)), bán kính (R) là :
$${(x - a)^2} + {(y - b)^2} = {R^2}$$
2. Nhận xét
Phương trình đường tròn ({(x - a)^2} + {(y - b)^2} = {R^2}) có thể được viết dưới dạng
$${x^2} + {y^2} - 2ax - 2by + c = 0$$
trong đó (c = {a^2} + {b^2} - {R^2})
( Rightarrow ) Điều kiện để phương trình ({x^2} + {y^2} - 2ax - 2by + c = 0) là phương trình đường tròn ((C)) là: ({a^2} + {b^2}-c>0). Khi đó, đường tròn ((C)) có tâm (I(a; b)) và bán kính (R = sqrt{a^{2}+b^{2} - c})
3. Phương trình tiếp tuyến của đường tròn
Cho điểm ({M_0}({x_0};{y_0})) nằm trên đường tròn ((C)) tâm (I(a; b)).Gọi (∆) là tiếp tuyến với ((C)) tại (M_0)
Ta có (M_0) thuộc (∆) và vectơ (vec{IM_{0}}=({x_0} - a;{y_0} - b)) là vectơ pháp tuyến cuả ( ∆)
Do đó (∆) có phương trình là:
$({x_0} - a)(x - {x_0}) + ({y_0} - b)(y - {y_0}) = 0$ (1)
Phương trình (1) là phương trình tiếp tuyến của đường tròn ({(x - a)^2} + {(y - b)^2} = {R^2}) tại điểm (M_0) nằm trên đường tròn.
4. Bài tập về phương trình đường tròn
Bài 1: Cho đường cong (Cm): x2+y2-2mx-4(m-2)y+6-m=0. Tìm điều kiện của m để (Cm) là phương trình đường tròn.
Lời giải:
Điều kiện để ((C_m)) là phương trình đường tròn là:
(eqalign{& {a^2} + {b^2} - c > 0 Leftrightarrow {m^2} + 4{left( {m - 2} right)^2} - left( {6 - m} right) > 0 cr& Leftrightarrow 5{m^2} - 15m + 10 > 0 Leftrightarrow left[ matrix{m > 2 hfill crm < 1 hfill cr} right. cr} )
Bài 2: Viết phương trình của đường tròn có tâm (Ileft( -3;4 right))và bán kính (R=2)
Lời giải:
Phương trình của đường tròn có tâm (I(-3;4)) và bán kính (R=2) là: ({{(x+3)}^{2}}+{{(y-4)}^{2}}={{2}^{2}}) hay({{(x+3)}^{2}}+{{(y-4)}^{2}}-4=0)
Bài 3: Phương trình nào sau đây là phương trình đường tròn?
A. ({{x}^{2}}+2{{y}^{2}}-4x-8y+1=0)
B. (4{{x}^{2}}+{{y}^{2}}-10x-6y-2=0)
C. ({{x}^{2}}+{{y}^{2}}-2x-8y+20=0)
D. ({{x}^{2}}+{{y}^{2}}-4x+6y-12=0)
Lời giải:
({{x}^{2}}+2{{y}^{2}}-4x-8y+1=0) không phải là phương trình đường tròn. Vì ({{x}^{2}}:{{y}^{2}}=1:2ne 1:2)
(4{{x}^{2}}+{{y}^{2}}-10x-6y-2=0) không phải là phương trình đường tròn. Vì ({{x}^{2}}:{{y}^{2}}=4:1ne 1:2)
({{x}^{2}}+{{y}^{2}}-2x-8y+20=0)có (a=1,,,b=4,,,c=20). Ta thấy (a,b,c)không thỏa mãn điều kiện ({{a}^{2}}+{{b}^{2}}>c). Đây không phải là một phương trình đường tròn.
({{x}^{2}}+{{y}^{2}}-4x+6y-12=0) có (a=2,,,b=-3,,,c=-12). Ta thấy (a,b,c) thỏa mãn điều kiện ({{a}^{2}}+{{b}^{2}}>c). Đây là một phương trình đường tròn.
Chọn đáp án D.
Bài 4: Phương trình ({{x}^{2}}+{{y}^{2}}-2x+4y+1=0) là phương trình của đường tròn nào?
Lời giải:
({{x}^{2}}+{{y}^{2}}-2x+4y+1=0) có hệ số (a=1,b=-2,c=2) sẽ có tâm (Ileft( 1;-2 right)) và (R=sqrt{{{left( -1 right)}^{2}}+{{2}^{2}}-1}=2)
Bài 5: Trong số các đường tròn có phương trình dưới đây, đường tròn nào đi qua gốc tọa độ(O(0,0))?
A. ({{x}^{2}}+{{y}^{2}}=1.)
B. ({{x}^{2}}+{{y}^{2}}-x-y+2=0)
C. ({{x}^{2}}+{{y}^{2}}-4x-4y+8=0.)
D. ({{(x-3)}^{2}}+{{(y-4)}^{2}}=25.)
Lời giải:
A. ({{x}^{2}}+{{y}^{2}}=1.) Thay (x=0,y=0) ta có ({{0}^{2}}+{{0}^{2}}=2) là mệnh đề sai.
B. ({{x}^{2}}+{{y}^{2}}-x-y+2=0). Thay (x=0,y=0) ta có (2=0) là mệnh đề sai.
C. ({{x}^{2}}+{{y}^{2}}-4x-4y+8=0.) Thay (x=0,y=0) ta có (8=0) là mệnh đề sai.
D. ({{left( x-3 right)}^{2}}+{{left( y-4 right)}^{2}}=25.) Thay (x=0,y=0) ta có ({{left( -3 right)}^{2}}+{{left( -4 right)}^{2}}=25) là mệnh đề đúng. Vậy ({{left( x-3 right)}^{2}}+{{left( y-4 right)}^{2}}=25.) đi qua gốc tọa độ.
Chọn đáp án D.
Bài 6: Viết phương trình đường tròn (C) có tâm (I(2;-4)) và đi qua điểm (A(1;3))
Lời giải:
Ta có: (R=IA=sqrt{{{left( 1-2 right)}^{2}}+{{left( 3+4 right)}^{2}}}=sqrt{50})
Phương trình đường tròn (C) có tâm (Ileft( 2;-4 right))có bán kính (R=sqrt{50}) là: ({{left( x-2 right)}^{2}}+{{left( y+4 right)}^{2}}=50.)
Bài 7: Xác định mối quan hệ giữa điểm (M(4;2)) và đường tròn ((C)) có phương trình ({{x}^{2}}+{{y}^{2}}-8x-6y+21=0)
Lời giải:
Đường tròn (left( C right)) có phương trình ({{x}^{2}}+{{y}^{2}}-8x-6y+21=0) sẽ có tâm (Ileft( 4;3 right)) bán kính (R=sqrt{{{4}^{2}}+{{3}^{2}}-21}=2).
Ta có (MI=sqrt{{{left( 4-4 right)}^{2}}+{{left( 2-3 right)}^{2}}}=1<R=2Rightarrow M) nằm trong (left( C right))
Bài 8: Viết phương trình đường tròn (C) có tâm (Oleft( 0;0 right)) và đi qua điểm (A(1;3))
Lời giải:
Ta có (R=OA=sqrt{{{left( 1-0 right)}^{2}}+{{left( 3-0 right)}^{2}}}=sqrt{10})
Phương trình đường tròn (C) có tâm (Oleft( 0;0 right)) có bán kính (R=sqrt{10}) là: ({{x}^{2}}+{{y}^{2}}=10.)
Bài 9: Viết phương trình đường tròn tâm I thuộc đường thẳng d có phương trình(x-2y+5=0) và đi qua hai điểm(Aleft( 0;4 right),,Bleft( 2;6 right))
Lời giải:
Giả sử điểm (Ileft( {{x}_{I}};{{y}_{I}} right)) là tâm của đường tròn (C). Vì I nằm trên đường thẳng (x-2y+5=0) nên ta có ({{x}_{I}}-2{{y}_{I}}+5=0,,,,,left( 1 right))
Vì đường tròn (C) đi qua hai điểm (Aleft( 0;4 right),,,Bleft( 2;6 right)) nên ta có (IA=IB). Điều này tương đương với (I{{A}^{2}}=I{{B}^{2}}) hay ({{left( {{x}_{I}} right)}^{2}}+{{left( 4-{{y}_{I}} right)}^{2}}={{left( 2-{{x}_{I}} right)}^{2}}+{{left( 6-{{y}_{I}} right)}^{2}}Leftrightarrow {{x}_{I}}+{{y}_{I}}-6=0,,,left( 2 right))
Từ (1) và (2) suy ra (left{ begin{array}{l}{x_I} - 2{y_I} + 5 = 0{x_I} + {y_I} - 6 = 0end{array} right. Leftrightarrow left{ begin{array}{l}{x_I} = frac{7}{3}{y_I} = frac{{11}}{3}end{array} right. Rightarrow Ileft( {frac{7}{3};frac{{11}}{3}} right)).
Mặt khác ta có (R=IA=sqrt{{{left( frac{7}{3} right)}^{2}}+{{left( frac{11}{3}-4 right)}^{2}}}=sqrt{frac{50}{9}})
Vậy (C) có dạng (left( C right):{{left( x-frac{7}{3} right)}^{2}}+{{left( y-frac{11}{3} right)}^{2}}=frac{50}{9})
Bài 10: Viết phương trình đường tròn (C) đi qua 3 điểm (A(1;4),B(-4;0)) và (C(-2;2))
Lời giải:
Phương trình đường tròn đi qua 3 điểm là: ({{x}^{2}}+{{y}^{2}}-17x+21y-84=0)
Link nội dung: https://diendanxaydung.net.vn/phuong-trinh-duong-tron-a35215.html