Toán 11 Bài 8: Phép Đồng Dạng Là Gì? Công Dụng Và Bài Tập Vận Dụng

1. Định nghĩa phép đồng dạng và công thức

Định nghĩa: Ta gọi phép biến hình F là phép đồng dạng tỷ số k (trong đó k>0) nếu với hai điểm bất kỳ M, N và ảnh tương ứng của M, N là M', N' ta đều có: M'N' = k . MN

$F(M)=M'; F(N)=N' Rightarrow M'N'=k.MN ( k>0)$

Nhận xét:

• Phép dời hình hay chính là phép đồng dạng với tỷ số k = 1

• Phép vị tự chính là phép đồng dạng với tỷ số k

• Sơ đồ biểu diễn mối quan hệ giữa phép đồng dạng, phép dời hình, phép vị tự:

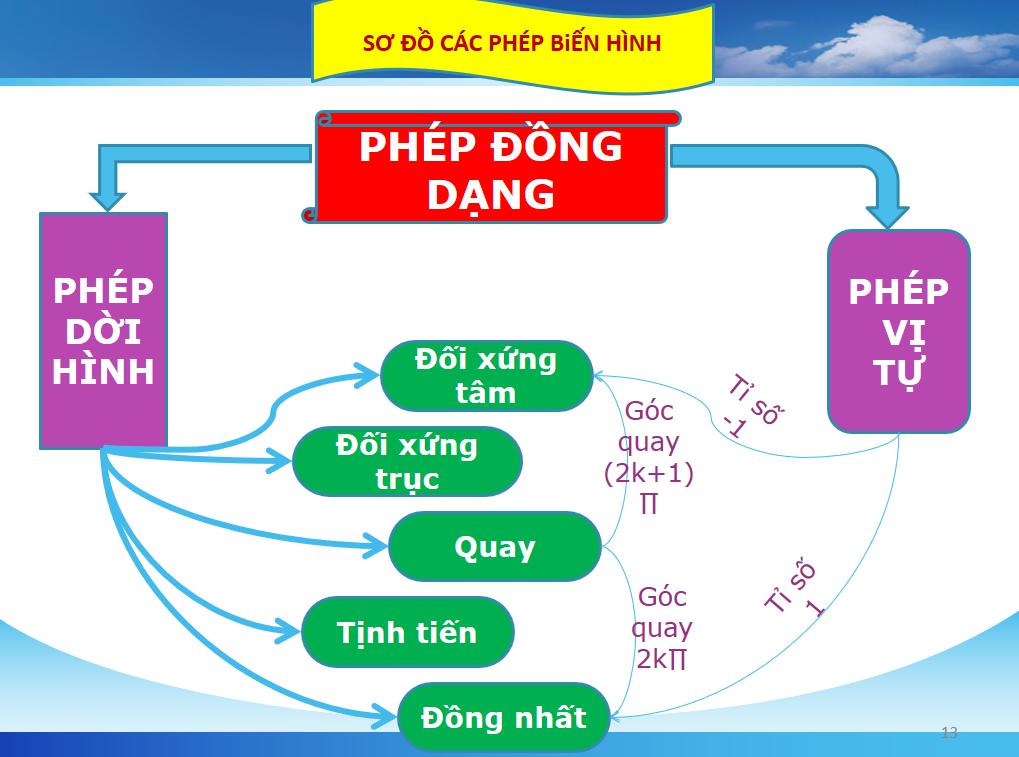
Lưu ý: Ta có thể nói phép đồng dạng là phép hợp thành của phép vị tự và phép dời hình. Hoặc có thể nói F là tích của V và D trong đó F là phép đồng dạng, V là phép vị tự, D là phép dời hình. Ký hiệu: F = DV.

Như vậy, để xác định ảnh của điểm M qua F ta có thể làm như sau:

Bước 1: Tìm ảnh $M_{1}$ của điểm M qua phép vị tự V

Bước 2: Tìm ảnh M' của điểm $M_{1}$ qua phép dời hình D

M' chính là ảnh của M qua phép đồng dạng.

Tham khảo ngay bộ tài liệu ôn tập kiến thức và tổng hợp toàn bộ phương pháp giải mọi dạng bài tập trong đề thi Toán THPT Quốc gia

2. Định lý phép đồng dạng

Phép đồng dạng F tỷ số k > 0 luôn là hợp thành của một phép vị tự V tỷ số k và một phép dời hình D.

3. Tính chất của phép đồng dạng

Ta có các hệ quả từ định lý trên như sau:

Phép đồng dạng F tỷ số k > 0:

• Biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không thay đổi thứ tự bạn đầu của 3 điểm.

• Biến một đường thẳng thành đường thẳng

• Biến 1 tia thành 1 tia

• Biến đoạn thẳng thành đoạn thẳng có độ dài được nhân lên k lần trong đó k là tỷ số của phép đồng dạng

• Biến 1 tam giác thành tam giác đồng dạng tỷ số k

• Biến 1 đường tròn có bán kính R thành đường tròn có bán kính bằng k . R

• Biến góc bằng với góc đó.

Nhận xét: Phép đồng dạng không có tính chất “biến đường thẳng thành đường song song hoặc trùng với nó” như phép vị tự.

4. Hai hình đồng dạng

4.1. Định nghĩa

Hai hình được gọi là đồng dạng nếu như có phép đồng dạng biến hình này thành hình còn lại.

4.2. So sánh phép dời hình, vị tự V(O,k), đồng dạng tỉ số k

• Giống nhau:

  • Đều biển 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự ban đầu của 3 điểm

  • Biến đường thẳng, tia, góc thành đường thẳng, tia, góc bằng nó

• Khác nhau:

Phép đồng dạng

Phép vị tự

Phép dời hình

- Biến một đoạn thẳng thành đoạn thẳng khác có độ dài được nhân lên k lần

- Biến 1 tam giác thành tam giác đồng dạng tỷ số k

- Biến 1 đường tròn có bán kính R thành đường tròn có bán kính bằng k .R

- Biến 1 đoạn thẳng thành đoạn thẳng có độ dài được nhân lên thêm

k lần

- Biến 1 tam giác thành tam giác đồng dạng tỷ số $left | k right |$

- Biến 1 đường tròn có bán kính

R thành đường tròn có bán kính bằng $left | k right | .R$

- Biến đoạn thẳng này thành đoạn thẳng khác có độ dài không thay đổi

- Biến tam giác này thành tam giác khác bằng với nó

- Biến đường tròn này thành đường tròn khác có bán kính không thay đổi

5. Một số bài tập về phép đồng dạng từ cơ bản đến nâng cao (có lời giải)

Bài 1: Cho một đường thẳng d: x - y + 1 = 0, d' là ảnh của d qua phép vị tự tâm I(1 : 1), k = 2 và phép tịnh tiến theo vectơ $overrightarrow{v}(-2;-1)$. Viết phương trình của d'?

Lời giải:

Bài 2: Cho đường tròn sau: (C): $(x - 1)^{2} + (y - 2)^{2}=4$. Tìm ảnh của (C) qua phép vị tự tâm O của (C) với tỷ số k= -2 và phép đối xứng qua trục Oy.

Lời giải:

Bài 3: Cho đường thẳng d trong mặt phẳng Oxy có phương trình là: x + y - 2 = 0. Thực hiện liên tiếp phép vị tự tâm I(-1;-1), k = 1/2 và phép quay tâm O một góc bằng $-45^{circ}$ được ảnh d' của d. Viết phương trình d'?

Lời giải: Gọi $d_{1}$ là ảnh của d qua phép vị tự tâm I(-1;-1), k = 1/2. Suy ra d'//d hoặc $d'equiv d Leftrightarrow d'$ có dạng: x + y + c = 0. Lấy điểm $M(1;1)epsilon d$:

$M'(x';y')=V_{(I;1/2)}(M)Rightarrow overrightarrow{IM'}=frac{1}{2}overrightarrow {IM} Leftrightarrow M'(0;0)epsilon d_{1}$

Phương trình của $d_{1}$ là x + y = 0. Ảnh của $d_{1}$ qua phép quay tâm O góc $-45^{circ}$ là d'.

Vậy phương trình d' là d' :x=0

Trên đây là tổng hợp toàn bộ kiến thức bài 8 phép đồng dạng trong chương trình Toán 11. Hy vọng các em đã nắm được lý thuyết đồng thời biết giải các bài tập liên quan đến phép đồng dạng. Đừng quên truy cập Vuihoc.vn để học thêm nhiều bài học bổ ích khác nhé!

Bài viết tham khảo thêm:

Phép vị tự

Đại cương về đường thẳng và mặt phẳng